CIVE 445 - ENGINEERING HYDROLOGY
CHAPTER 4B: HYDROLOGY OF SMALL CATCHMENTS, OVERLAND FLOW

1.2 OVERLAND FLOW

Overland flow is surface runoff that occurs in the form of sheet flow on the land surface without concentrating in clearly defined channels.
Overland flow is the first manifestation of surface runoff.
Overland flow uses conceptual and deterministic methods to describe surface runoff in overland flow planes.
In overland flow applications, effective rainfall is referred to as rainfall excess.
Overland flow can account for runoff concentration and diffusion, and produces a hydrograph reflecting these two properties combined.
Rainfall can be allowed to vary in space and time if necessary.
Overland flow theory is more complex that the rational method.
It solves the problem of hydrograph shape very well.
For small catchments, the peak flow calculated by overland flow is the same as that of the rational method.
In a modeling framework, with many overland flow modules, the calculated peak flow has more detail than that of the rational method.
Overland flow applies to small catchments, but can also be applied with care to midsize catchments.
Small modules will retain topographic details.
Larger modules may mask the distributed character of overland flow.
Overland flow requires a computer to perform the calculations.

Overland flow theory

The equation of mass conservation is:

∂Q/∂x + ∂A/∂t = 0

Inclusion of sources and sinks leads to:

∂Q/∂x + ∂A/∂t = q_L

This equation is expressed on the overland flow plane per unit of width:

∂q/∂x + ∂h/∂t = i

Flow over the plane can be described as follows:

Fig. 4-9

As excess rainfall begins, water accumulated on the plane surface and begins to flow out of the plane at its lower end.
Flow at the outlet increase gradually from zero, while the total volume of water stored over the plane also increases gradually.
If rainfall excess continues, both outflow and total volume of water stored over the plane reach a constant value.
Outflow and storage volume remain constant and equal to the equilibrium value.
Immediately after excess rainfall ceases, outflow begins to draw water from storage, gradually decreasing while depleting the storage volume.
Eventually, outflow returns to zero as the storage volume is completely drained.

Fig. 4-10

At equilibrium state, the outflow must equal the inflow. Therefore:

q_e = (i/3600) L

in which:

q_e= equilibrium outflow in L/s/m
i = rainfall excess in mm/hr
L = plane length in m.

This equation is a statement of runoff concentration.
The equilibrium storage volume is the area above the rising limb and below a line q = q_e.
As a first approximation, it can be assumed to be equal to:

S_e = (q_e t_e)/2

in which:

S_e= equilibrium storage volume in L/m
q_e= equilibrium outflow in L/s/m
t_e = time to equilibrium in seconds.

Irregularities cause the equilibrium state to be approached asymptotically, and the actual time to equilibrium is not clearly defined.
A value of t corresponding to q = 0.98 q_e may be taken as an approximation.
Equations of continuity and motion: Equations 4-21 and 4-22.
Solutions can be attempted with:

Storage concept of Horton and Izzard (conceptual) (1940's)
Kinematic wave technique of Wooding (deterministic) (1960's)
Diffusion wave technique (1990's) (Ponce, 1986; HEC-1, 1990 ; HEC-HMS, 1998)
Dynamic wave technique (Ben-Zvi) (1970's).

Overland flow solution based on storage concept

Horton noticed that experimental data justified a relationship between equilibrium outflow and equilibrium storage as follows:

q_e = a S_e^m

in which a and m are empirical constants.
A mean flow depth is defined as follows:

h_e = S_e / L

Combination of these equations leads to:

q_e = b h_e^m

in which b = a L^m, another constant.
Typical values of the rating exponent m are shown in the following table.

Table 4-3

From the previous equations, an estimate of time to equilibrium is:

t_e = 2 / { q_e^[(m-1)/m] a^(1/m) }

For laminar flow conditions, b = a L^m = C_L, where C_L is

C_L = g S_o / (3 ν)

The time to equilibrium under laminar flow is:

t_e = (2 L ^1/3) / [ i^2/3 C_L^2/3 ]

For turbulent flow conditions, b = a L^m = (1/n) S_o^1/2.
The time to equilibrium under mixed laminar-turbulent and fully turbulent conditions is:

t_e = 2 (nL)^1/m / { i^(m-1)/m S_o^[1/(2m)] }

To derive the preceding equation, combine the following equations:

q_e = i L    (Continuity)

S_e = (q_e t_e)/2    (Horton's assumption for equilibrium storage)

h_e = S_e / L    (equilibrium flow depth based on equilibrium storage)

q_e = (1/n) S_o^1/2 h_e^m    (turbulent Manning flow rating)

Notice that time to equilibrium increases with friction and plane length, and decreases with rainfall intensity and plane slope.
This is the same form as Papadakis and Kazan's 1987 formula for time of concentration.
The friction parameter is similar to Manning's, but can accomodate mixed laminar-turbulent flow.
For that purpose, it is also referred to as N.
Typical values of N are shown in the following table.

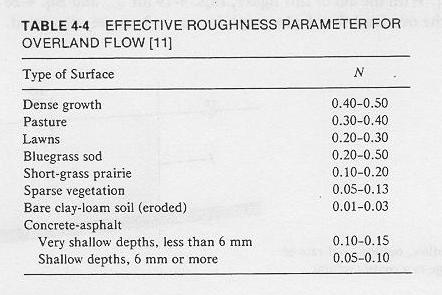
Table 4-4

The Horton-Izzard solution is based on the assumption that the discharge-storage rating is valid not only at equilibrium but also at any other time.

q = a S^m

This assumption is convenient because it allows an analytical solution for the shape of the overland flow hydrograph.
The generic discharge-storage equation represents a nonlinear reservoir, replacing the equation of motion.
Horton's overland flow model is shown in page 140.
Horton's solution is for m = 2 (mixed laminar-turbulent flow); Izzard's is for m = 3 (laminar flow).
The graphical form of Izzard's overland flow model is shown in page 141.

Overland flow solution based on kinematic wave theory

According to this theory, the equation of motion can be approximated by a depth-discharge rating of the form:

q = b h^m

in which b and m are empirical constants.
Unlike Horton's approach, which is based on reach volume data, the kinematic wave approach bases the rating on cross-sectional data such as flow depth.
The Horton approach is lumped; the kinematic wave approach is distributed.

The difference between a rating based on storage vs one based on flow depth merits careful analysis.
There are two distinct features in natural catchments:

reservoirs, and
channels.

In an ideal reservoir, the water surface slope is zero, and therefore, outflow and storage are uniquely related.
Outflow can be uniquely related to storage volume, stage and flow depth.
In an ideal channel, the water surface slope is nonzero, and storage is a nonunique function of both inflow and outflow.
At any cross section, discharge can only be related to flow depth.
In the Horton approach (reservoir), outflow is related to storage, and by extension, to the mean flow depth on the overland flow plane.
In the kinematic approach (channel), outflow is related to its flow depth.
The typical overland flow problem has a nonzero water surface slope; it should behave more as a channel that a reservoir.
It would appear that the kinematic approach is better suited since it simulates channels bettter than reservoirs.
However, the kinematic approach lacks runoff diffusion, while there is diffusion in the storage concept.
When diffusion is at issue, the storage concept is better than the kinematic wave.

The kinematic wave assumption amounts to substituting a uniform flow formula for the equation of motion.
It says that, as far as momentum is concerned, the flow is steady!
However, the unsteadiness is preserved through the continuity equation.
The implication of kinematic flow is that unsteady flow can be visualized as a sucession of uniform flows, with the water surface slope remaining constant at all times.
This can be reconciled with reality only if the changes in stage occur very gradually.
The changes in momentum should be negligible compared to the forces driving the steady flow (gravity and friction).
The kinematic flow number of Woolhiser and Liggett determines whether a flow can be considered kinematic or not.

The kinematic wave model is shown in page 143 and page 144.
The time to equilibrium of kinematic flow is:

t_k = (nL)^1/m / { i^(m-1)/m S_o^[1/(2m)] }

This is the same as Horton's mixed laminar-turbulent equation, but without the factor 2.
The analytical solution to the kinematic wave, a deterministic model, is a parabola, with no diffusion.
The analytical solution to Horton's conceptual model is a hyperbolic tangent.
See graphical comparison of dimensionless overland flow hydrographs.
Very important: Lack of diffusion means that the kinematic wave is about twice as fast as the storage concept solution.
Woolhiser and Liggett's kinematic flow number is:

K = (S_o L) / (F² h_o)

in which F = Froude number.
Values of K greater than 20 describe kinematic flow.

The steeper the slope, the greater the K value, and the more kinematic the flow is.
Other variables in definition of kinematic flow number are secondary.
The kinematic wave solution accounts for only friction slope and plane slope.
For very mild plane slopes, the neglected terms (pressure gradient and inertia) may be promoted to the point where neglect is no longer justified.
Most overland flow have steep slopes, usually greater than 0.01.
Rule of thumb: any slope greater than 0.01 (1 percent) is kinematic.
For slopes of about 0.0001, the kinematic wave may not be sufficient.

The kinematic wave celerity varies with the flow, making the kinematic wave a nonlinear equation.
This property leads to a steepening tendency (inbank flows).
Analytical solutions, if carried long enough, lead to the kinematic shock, due to the steepening of the kinematic wave.
In nature, small irregularities produce diffusion, which arrests the steepening.
Numerical solutions have numerical diffusion, which also arrests the steepening.
If the solution is perfect, with no irregularities or errors, it will eventually develop into a shock.
Due to natural irregularities, kinematic shock may be a rare occurrence in nature.

Overland flow solution based on diffusion wave theory

According to diffusion theory, the flow depth gradient is largely responsible for the diffusion mechanism.
Its inclusion in the analysis provides runoff concentration with diffusion.
Diffusion wave equations: page 146 and page 147.
The hydraulic diffusivity is:

ν_h = (u_o h_o) / (2 S_o)

in which u, h, and S are mean velocity, flow depth and channel slope, respectively.
For very small values of slope, channel diffusivity is very large.
For zero slope (horizontal channel), the equations ceases to apply.
For realistic slopes in the range 0.001-0.0001 the diffusion component can be quite significant.
Diffusion waves apply for the milder slopes for which the kinematic wave is not applicable.

Summary

Overland flow can provide more detail than the rational method.
This increased detail is at a cost of increased complexity.
Overland flow is suited for computer applications.
However, the problem of conversion of rainfall to runoff is not just one of overland flow.
It also includes the abstraction from total rainfall to effective rainfall (see Runoff curve number method in Chapter 5).

Go to Chapter 5A.

050223